在行测考试中，排列组合问题经常出现，大多数学生对于这类题目总是望而生畏，但其实如果了解了其中的相应逻辑关系，很多问题就迎刃而解了。在排列组合问题中，有一类隔板模型的题目，如果能够掌握题目特征和对应的公式，问题就可以顺其自然地解决了。下面，山东公务员考试网（www.sdgwy.org）就和大家一起来学习一下。

　　隔板模型的本质其实是相同元素的不同分堆，解决隔板模型的问题，我们需要了解对应的公式：把n个相同的元素分给m个不同的对象，每个对象至少分得1个元素，一共有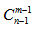种分法。

　　不过，隔板模型的应用需要满足以下条件：首先，所要分的元素必须完全相同;其次，所要分的元素必须分完，决不允许有剩余;最后，每个对象至少分到一个，决不允许出现分不到元素的对象。只要同时满足了以上三个条件，就可以直接使用隔板模型的公式。

　　接下来我们通过两道题目来看一下隔板模型问题的应用。

　　例1.有10本相同的杂志要分给三个不同的阅读室，要求每个阅读室至少分一本，有多少种方法?

　　A.36 B.45 C.72 D.90

　　【答案】A。解析：题目所描述的是相同的10本杂志分给三个不同的阅读室，是属于相同元素的不同分堆，且满足隔板模型的三个条件，属于隔板模型问题。题干要求每个阅读室至少分一本，因此一共有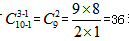种方法，故选择A选项。

　　例2.将10张“200元代金券”分给部门的3位先进工作者，每人至少分2张，则有多少种不同的分配方案?

　　A.10 B.15 C.22 D.30

　　【答案】B。解析：题目所描述的是相同的10张代金券分给3位先进工作者，是属于相同元素的不同分堆，但是不满足隔板模型的“每个对象至少分一个”这一条件，但是我们可以通过转换使之满足，即先给每位先进工作者1张代金券，剩下7张代金券，分给3位先进工作者且每人至少1张，利用公式，一共有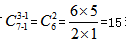种方法，故选择B选项。

　　对于隔板模型而言，需要了解其应用环境以及公式，如果应用环境不满足，可以通过转换条件使之满足，相信各位同学通过上面两道题目已经掌握了隔板模型在具体题目中的应用，希望各位同学都能够举一反三，熟练掌握，在考试中抓住这一部分题目，拿到分数。