做过图形推理的考生都知道,图形题不难,难就难在如何快速破题,找对考点方向。这里总结了图形推理常考的考点及对应的破题技巧,并附上相应的考题。
一、图形组成相同看位置
1. 动态位置变化
(1)特点:元素本身大小 形状不变,变的是方向 距离等
(2)移动
原则:就近 平均原则
移动方向:上下 左右 折返 循环 顺逆时针
(3)旋转 翻转
判别方法:
①时针法(方向一致为旋转,否则是翻转)
②箭头法:(判断旋转方向,角度)
(4)注意:旋转和翻转后的图形一致,是有可能的
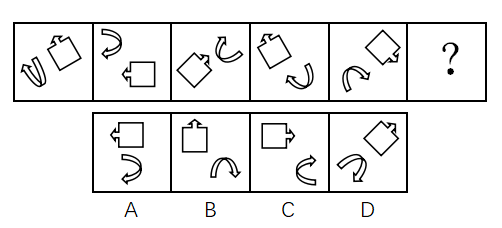
答案:C
2. 静态位置变化
(1)特征:元素位置不变,图中元素的相对位置呈现某种规律
(2)图形相对位置
相离:上下 左右 相邻 相隔
相交:相交关系 相交形状 相交面积
相切:外切 外接 内切 内接
包含:内外位置(尤其注意内外为直 曲图形的情况)
(3)点、线的位置
点的遍历、点的位置不重合
点、线的相对位置关系
点与点的相对位置
线与线的关系:平行、相交、垂直等
点或线与其他图形的相对位置,如点接、线接、点在锐角旁
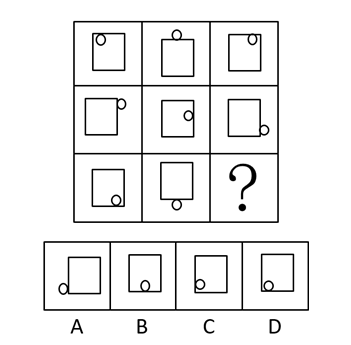
答案:D
二、图形组成相似看样式
1. 叠加
(1)常规考法:去异存同 去同存异
(2)特别考法:黑白叠加 米字型
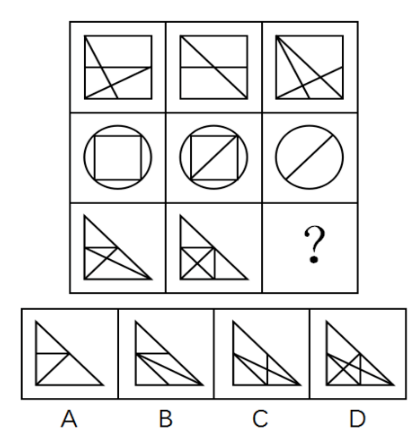
答案:C
2. 遍历
(1)单元素遍历:不同图中都出现某元素(乱中求同)
(2)整体遍历:以行/列为单位,元素整体相同(缺啥补啥)
(3)局部遍历:相邻图形中有某个元素相同(相邻求同)
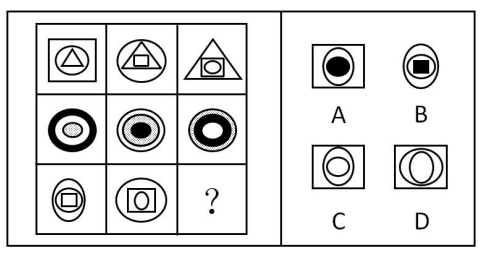
答案:C
三、图形组成凌乱看属性
1. 曲直性
(1)图形主要由线构成
(2)常见考法:
①都是直线/曲线
②直线曲线交替,或内外交替
2. 封闭性
(1)图形有明显的封闭空间,即面
(2)常见考法:
①都是封闭/开放/半开放图形
②封闭 开放 半开放图形交替出现
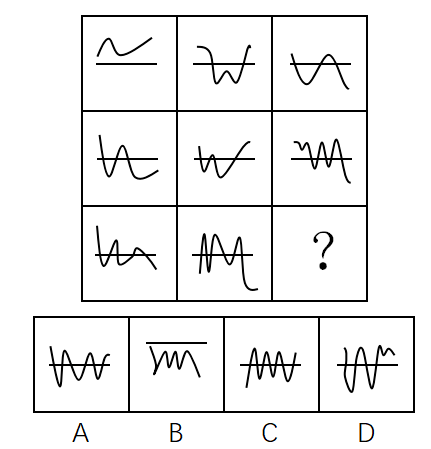
答案:C
3. 对称性
(1)出现明显的轴对称 中心对称图形,如五角星
(2)常见考法:
①都是轴对称、中心对称图形,或同时两者兼具
②轴对称、中心对称图形,非对称图形等交替出现

答案:C
4. 角
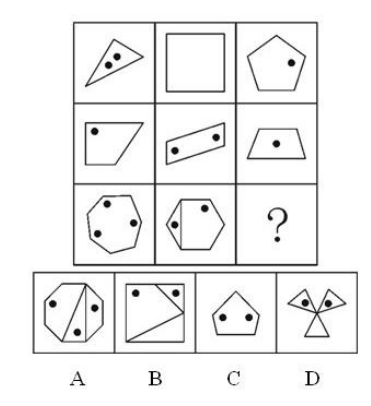
答案:D
5. 重心
6. 凹凸性
注意:是图形的任一条边都符合(曲线图形需做切线)
四、属性不行看数量
1. 常规考点
(1)属性:点 线 面
(2)数量规律:相同 自然数列 递增递减 递推等
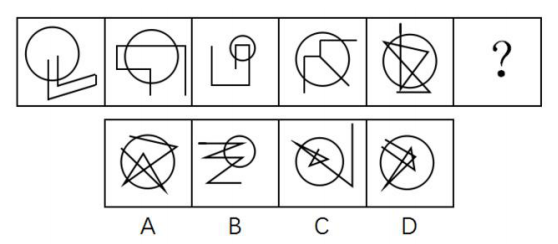
答案:C
2. 特殊考点
(1)角:相同 递增 递减等
(2)元素:种类数相同 递增 递减等

A.①④⑥,②③⑤ B.①③⑤,②④⑥
C.①②④,③⑤⑥ D.①⑤⑥,②③④
答案:A
五、一笔画
1. 定义
一笔画图形:一笔画成,路径不重复,不中断的线条图形
奇点:连接奇数条线(直线或曲线)的点
2. 方法
笔画数=奇点数/2
奇点:端点、T字交点;
偶点:角 十字交叉点
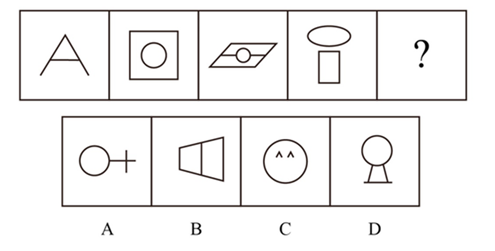
答案:A
六、空间重构有妙招
六面体: 时针法 公共边法 橡皮法
四面体:左右面 公共边 公共点法
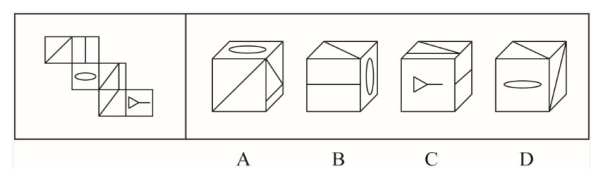
答案:C
七、其他考点
1. 汉字 字母 数字类
面 对称

答案:C
2. 三视图
主视图 俯视图 左视图
哪一项不可能是该多面体的视图( )
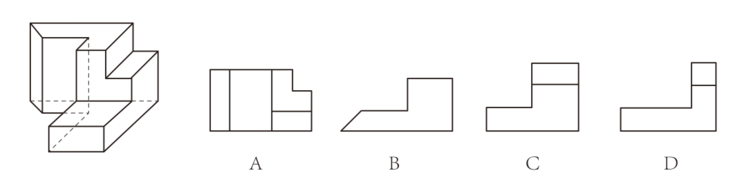
答案:D
3. 截面图
做题时注意积累各种截面
4. 实体重组
5.拆/拼纸板
题干入手:优先拼接相同的边
选项入手:特殊的角,在题干中是否有对应图形等
题:边四个图形中,只有一个是由左边的四个图形拼合(只能通过上、下、左、右平移)而成的,请把它找出来:
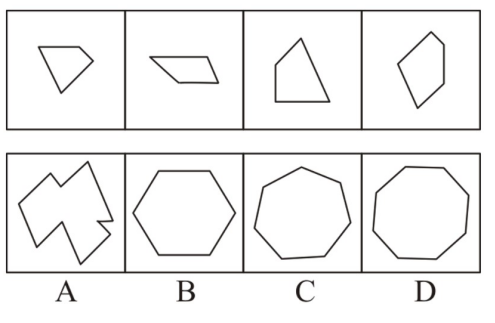
答案:D
以上就是本次整理的图推常考考点,上面的的这些题目你都答对了吗?










