三个集合容斥问题是公务员考试的常考题型，大部分考生虽然熟知三集合容斥问题的常用公式A∪B∪C=A＋B＋C－A∩B－B∩C－A∩C＋A∩B∩C，但是不一定能把题目做对，究其原因是没有理解公式的准确含义。下面通过一道典型例子讲解下蕴含在这个公式下的深层次含义。

　　【例】

　　某公司组织运动会，据统计，参加百米跑项目的有86人，参加跳高项目的有65人，参加拔河项目的有104人。其中，至少参加两种项目的人数有73人，三项都参加的有32人。则该公司参赛的运动员有（  ）人。

　　A．89        B．121       C．150        D．185

　　【错误解析】

　　设参加百米跑、跳高、拔河项目的运动员分别构成集合A、B、C，运用三集合容斥问题公式“A∪B∪C=A＋B＋C－A∩B－B∩C－A∩C＋A∩B∩C”求解。由A∩B+B∩C+A∩C表示的是参加两种项目的总人数，可得A∩B+B∩C+A∩C=73-32=41。而A∩B∩C=32，则A∪B∪C=86+65+104－41+32=246（人）。没有答案。

　　【错解门诊】

　　上述解法虽然选对了公式，但是没有算出正确答案，其最大的错误在于没有真正理解A∩B+B∩C+A∩C的含义。

　　A∩B+B∩C+A∩C=只参加两种项目的人数+3×参加三种项目的人数。而至少参加两种项目的人数有73人=只参加两种项目的人数+参加三种项目的人数。两式对比发现，前式比后式多了“2×参加三种项目的人数”。

　　【正确解析】

　　选C。设参加百米跑、跳高、拔河项目的运动员分别构成集合A、B、C，根据三集合容斥问题公式A∪B∪C=A＋B＋C－A∩B－B∩C－A∩C＋A∩B∩C，A∩B+B∩C+A∩C=73+2×32=137，A∩B∩C=32，则A∪B∪C=86+65+104-137+32=150（人）。

　　【指点迷津】

　　对于三个集合容斥问题，建议画出文氏图来辅助求解。具体操作过程如下：

　　确定分类标准→把集合对应圈圆→确定各圆圈位置关系→确定各集合逻辑、数量关系。

　　一般地，三个集合容斥问题的文氏图如下：

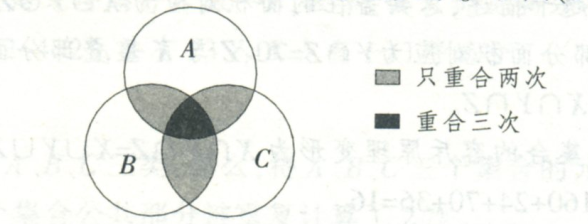
　　上图中需要注意的是：A∩B+B∩C+A∩C=只重复两次的情况+3×重复三次的情况。

　　这样，A∪B∪C=A＋B＋C－A∩B－B∩C－A∩C＋A∩B∩C=三个圆各自情况之和－只重复两次的情况－2×重复三次的情况。

　　从上述解析中可以看出，对于容斥问题，仅仅通过背背、套套公式是不能解决问题的，而是要真正理解公式所表达的含义，只能这样才能做到举一反三，不会出现“本来会做，但是换种说法就不会做”的情况。

　　>>>点击可进入争议易错题专栏

　　欢迎扫描下方二维码加入山东公务员考试网（http://www.sdgwy.org/）微信平台。