时钟问题是公考常考的题型之一,其中有一类坏时钟问题让不少考生感到头大。考生常常感觉自己已经完全理解了题意,也算出了答案,却在最后发现做错了,不禁困惑哪里出了问题。下面通过一道典型例题来剖析一下此类问题的误区所在。
【例】
有一只坏时钟,每小时慢3分钟,早晨4点30分的时候,把钟对准了标准时间,则钟走到当天上午10点50分的时候,标准时间是多少( )
A.11点整 B.11点9分 C.11点10分 D.11点12分
【错误解析】
选B。从4点30分到10点50分,坏时钟总共走过了6小时20分。由于坏时钟每小时慢3分钟,所以得出总共慢了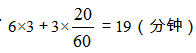 ,10点50分往后推19分钟,即是11点9分,因此B项正确。
,10点50分往后推19分钟,即是11点9分,因此B项正确。
【错解门诊】
上述解法错误之处在于偷换了概念。当坏钟钟面时间走过1小时时,实际时间不会正好走过1小时3分钟的,因为这多走的3分钟也有走慢的成分。正如实际上走1小时,钟面时间只走了57分钟,而钟面时间走3分钟,实际时间相当于走了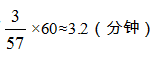 ,即钟面上走1小时,实际时间走了1小时3.2分钟。因此按照上述算法算得的计算结果比正确答案小了一些。
,即钟面上走1小时,实际时间走了1小时3.2分钟。因此按照上述算法算得的计算结果比正确答案小了一些。
【正确解析】
选C。每小时慢3分钟→坏时钟时间︰标准时间=57︰60。
坏时钟从4点30分到10点50分,总共走过了6小时20分,合为380分钟。
假设标准时间走了x分钟,那么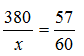 ,则x=400(分钟)。
,则x=400(分钟)。
说明标准时间比坏时钟显示快400-380=20(分钟),标准时间应为10点50分往后推20分钟,即11点10分。因此C项正确。
【指点迷津】
坏时钟问题,主要涉及到坏时钟时间和标准时间之间的比例关系,根据上述解析可以看出,其本质上是比例问题。
坏时钟时间与标准时间的比例关系为:
每小时快N分钟,则标准时间的1小时即60分钟中,快时钟走(60+N)分钟,快时钟时间︰标准时间=(60+N)︰60。
每小时慢N分钟,则标准时间的1小时即60分钟中,慢时钟走(60-N)分钟,慢时钟时间︰标准时间=(60-N)︰60。
假设快时钟显示的T1到T2这段时间为x分钟,标准时间走过了y分钟,则根据(60+N)︰60=x︰y,可求得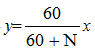 ,根据经过的标准时间可以求得T2对应的实际时间。
,根据经过的标准时间可以求得T2对应的实际时间。
通过上述比例关系可以看出,此类问题都是与1个小时即60分钟作对比,切忌不要把每分钟作为基数进行比例运算。
坏时钟问题本身并非计算量特别大的题目,也不是特别难理解的题目,解答这类问题时考生首先要克服自己的心里障碍,不要一遇到困难就一筹莫展。只有充分理解时钟运转过程中所蕴含的数量关系,找到坏时钟时间与标准时间之间的比例关系,才能迎刃而解。
>>>点击可进入争议易错题专栏
欢迎扫描下方二维码加入山东公务员考试网(http://www.sdgwy.org/)微信平台。










