1.甲、乙两辆型号不同的挖掘机同时挖掘一个土堆，连续挖掘8小时即可将土堆挖平。现在先由甲单独挖，5小时后乙也加入挖掘队伍，又过了5小时土堆被挖平。已知甲每小时比乙能多挖35吨土，则如果土堆单独让乙挖，需要多少个小时？

　　A.10

　　B.12

　　C.15

　　D.20

　　2.打印一份稿件，小张5小时可以打完这份稿件的1/3，小李3小时可以打完这份稿件的1/4，如果两人合打多少小时可以完成？（  ）

　　A.6

　　B.20/3

　　C.7

　　D.22/3

　　3.由甲、乙、丙三个工程队分别承担工程量之比为5：4：2的三项工程，同时开工，若干天后，甲未完成的工作量是乙所完成的工作量的3倍，乙未完成的工作量是丙所完成的工程量的2倍，丙未完成的工作量等于甲所完成的工作量，则甲、乙、丙的效率之比为多少?(    )

　　A.5：10：9

　　B.3：5：4

　　C.8：6：7

　　D.5：4：2

　　4.工程队计划150天完成建筑，现计划30天后新增设备，提高20%工作效率，可以提前几天完成?（    ）

　　A.20

　　B.25

　　C.30

　　D.45

　　5.两工厂各加工480件产品，甲工厂每天比乙工厂多加工4件，完成任务所需时间比乙工厂少10天。设甲工厂每天加工产品x件，则x满足的方程为（  ）。

　　A.480/x＋10＝480/(x＋4)

　　B.480/x－10＝480/(x＋4)

　　C.480/x＋10＝480/(x－4)

　　D.480/x－10＝480/(x－4)

　　山东公务员考试网（www.sdgwy.org） 题目或解析有误，我要纠错

　　1.答案: D

　　解析: 根据题意，甲每小时比乙多挖35吨，可假设甲的效率是x+35，乙的效率是X。由“甲乙一起挖8小时可挖完”可知工作总量为：8（x+x+35）;再由“甲先挖5小时，乙也加入，再挖5小时可挖完”可知工作总量为：5（x+35)+5(x+x+35)，由此可得方程8（x+x+35）=5（x+35)+5(x+x+35），解得x=70。则有乙单独挖完需要8*（70+70+35）/70=20小时。

　　2.答案: B

　　解析:

　　设总的稿件为60张，由题意，小张每小时打印1/15，小李每小时打印1/12，则小张、小李每小时分别能打印4张、5张。如果两个人合打，每小时打印9张，则打印完这份稿件需要 60÷9＝20/3（小时），故正确答案为B。

　　3.答案: A

　　解析:

　　设三项工程的工程量分别为5，4，2，甲、乙、丙分别完成了工程。则有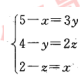，x：y：z=5:10:9。

　　4.答案: A

　　解析:

　　赋值“未提高之前的工作效率”为“1”，工作总量=工作效率×工作时

　　间=1×150=150，按原工作效率工作的总量是：1×30=30，则剩余工作总量是：

　　150-30=120；提高后的工作效率是：1×120%=1.2，完成剩余工作总量需要的天

　　数：120÷1.2=100（天）；可提前完成的天数=计划天数-实际天数=150-（100+30）

　　=20（天），因此，本题答案选择A选项。

　　5.答案: C

　　解析:

　　根据题意得：甲完成需要480/x天，乙完成需要480/（x－4） 天，则完成时间的等量关系为480/x＋ 10＝480/（x－4）。故正确答案为C。