【例题】某公司为客户出售货物，收取3%的服务费；代客户购置设备，收取2%的服务费，某客户委托该公司出售自产的某种物质并为购置新设备。已知公司共收取该客户服务费200元，客户收支恰好平衡，则自产的物品销售价是多少元？
　　A．3380         B．4080     C．3920       D．7960

　　【例题】有20位运动员参加长跑，他们的参赛号码分别是1、2、3、……、20，至少要从中选出多少个参赛号码，才能保证至少有两个号码的差是13的倍数？
　　A.12          B.15    C.14    D.13

　　【例题】A、Ｂ两村庄分别在一条公路Ｌ的两侧，Ａ到Ｌ的距离｜ＡＣ｜为１公里，Ｂ到Ｌ的距离｜ＢＤ｜为２公里，Ｃ、Ｄ两处相距６公里，欲在公路某处建一个垃圾站，使得Ａ、Ｂ两个村庄到此处处理垃圾都比较方便，应建在离Ｃ处多少公里？

　　
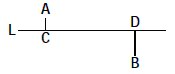
　　Ａ．2.75    Ｂ．3.25            Ｃ．2    Ｄ.3

　　【例题】一副扑克牌有52张，最上面一张是红桃A，如果每次把最上面的10张移到最下面而不改变它们的顺序及朝向，那么，至少经过多少次移动，红桃A会出现在最上面？
　　A．27           B．26         C．25    D．24

　　【例题】某市2009年末汽车保有量为50万辆，预计此后每年报废上一年末汽车保有量的5%，并且每年新增汽车数量相等，如要求该市汽车保有量不超过200万辆，那么每年新增汽车数量不应超过多少万辆？
　　A．2.5             B．5         C．7.5          D．10

　　山东公务员考试网(http://www.sdgwy.org/）解析

　　【解析】B。设自产物品售价为x，购置新设备费用为y。则客户收入为97%x，支出为（1+2%）y，根据收支平衡97%x=（1+2%）y。总服务费3%x+2%y=200，解得x=4080元。

　　【解析】C。抽屉原理。将20个号码分成{1，14}、{2，15}、{3，16}、{4，17}、{5，18}、{6，19}、{7，20}、{8}、{9}、{10}、{11}、{12}、{13}这13个集合，从任意两个不同集合中取出的两个数相差都不为13，根据抽屉原理1，至少选出13+1=14个号码，才能保证至少有两个号码的差是13的倍数。
　　快速突破:采用最差原则，1-13都不能满足任意两者差是13，这时随意再加一个数能够保证至少有两个号码的差是13，选C。

　　【解析】B。若使A、B两村庄到此地处理垃圾都很方便，需要使得两者到垃圾站的距离相等。
 　　
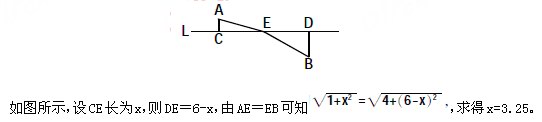
　　快速突破:已知AE＝EB，AC＜DB，则CE＞ED，即CE＞3，结合选项得CE＝3.25。

　　【解析】B。移动5次后红桃A上面有2张牌，每移动5次都会多出2张。这样移动5×5=25次后红桃A上面累计有10张牌，再移动1次红桃A就会再次出现在最上面。因此，至少移动5×5+1=26次后，红桃A会出现在最上面，选B。
　　快速突破:设至少移动x次，要使红桃A再次出现在最上面，则移动的总牌数应该是52的倍数，即10x为52的倍数，选项中只有x=26满足条件。

　　【解析】D。当该市汽车保有量为200万辆时，报废的汽车最多，为200×5%=10万辆，只要新增汽车数量不超过10万辆，此时该市汽车保有量不超过200万辆。选D。