【例题】五对夫妇排坐一长桌，要求夫妇相邻而坐，且同性别的相间而坐，问有多少种坐法？
　　A．24         B．120            C．240        D．14400

　　【例题】袋子里红球与白球的数量之比为19∶13，放入若干个红球后，红球与白球的数量之比变为5∶3，再放入若干个白球后，红球与白球的数量之比为13∶11，已知放入的红球比白球少80个。那么原来袋子里共有多少个球？
　　A.650        B.720       C.840          D.960

　　【例题】现有30ml和40ml的试管各一个，纯净水和纯酒精各2000ml。现在需要在大烧杯里配置某种酒精溶液150ml，其中酒精和水的体积比为1∶2。若倒进或者倒出溶液都算一次操作，则最少需要多少次操作才能满足要求？
　　A．10          B．11          C．12         D．13

　　【例题】有A、B、C三支球队进行循环赛，每两队之间各赛一场，胜一场得3分，平一场得1分，负一场得0分。已知A队总进球数为0，平了1场；B队净胜球数为-2，胜了一场。则C队得了（    ）分。
　　A.0           B.1            C.4           D.6

　　【例题】将大米300袋、面粉210袋和食用盐163袋按户分发给某受灾村庄的村民，每户分得的各种物资均为整数袋，余下的大米、面粉和食用盐的袋数之比为1∶3∶2，则该村有多少户村民？
　　A．7              B．9          C．13             D．23

　　山东公务员考试网(http://www.sdgwy.org/）解析

　　【解析】C。第一个位置在10种坐法，第三个位置有4种坐法，第五个位置有3种坐法，第七个位置有2种坐法，第九个位置有1种坐法，其余位置坐着奇数位置相应配偶，因此一共有10×4×3×2×1＝240种坐法。

　　【解析】D。第一次放入若干个红球，白球数量不变，比例由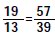变为

　　有红球57份，白球39份，增加的红球为65-57＝8份，增加的白球为55-39＝16份，放入的红球比白球少80个，对应16-8＝8份，所以每份为80÷8＝10个球，原来共有球（57+39）×10＝960个。

　　【解析】B。需要纯酒精150÷（2+1）＝50ml，纯净水150-50＝100ml。
　　取100ml的水，100＝30+30+40，因此，需要3×2＝6次操作；　
　　取50ml的酒精，50＝40+40-30，因此，需要2+2+1＝5次操作。
　　共需要6+5＝11次操作。具体操作如下：

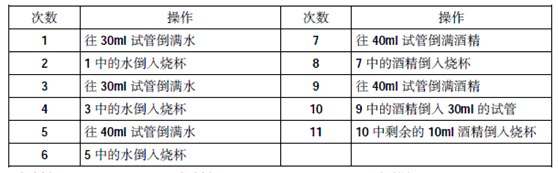
　　【解析】C。这三支球队每只球队都赛了2场，一共赛了3场。A队总进球数为0，且平了一场，说明A队平一场，负一场；如果A队和B队的比赛为平局，则B队胜一场，平一场，这与B队净胜球数为-2矛盾；故A队与C队的比赛为平局，A队负于B队，由于B队净胜球为负的，则B队负于C队。综上，C队胜一局，平一局，一共得了4分

　　【解析】D。本题相当于300、210、163除以户数的余数之比为1∶3∶2。代入选项判断，只有D符合条件。