【例题】某班进行数学测试，共考3题，每题的评分是０、１、2、3、4、5、６、７，有一群学生每人得分的乘积都是3６，而且任意两人各题得分不完全相同，那么这群学生最多有多少人？
　　A.12    B．15     C.16      D.18

　　【例题】有16个盒子，里面放了27个小球，每个盒子放了1个、2个或者3个小球，其中放1个小球的盒子数与放2个和3个小球的盒子总数一样多，问放2个小球的盒子有多少个？
　　A．3       B．4         C．5        D．6

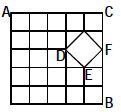
　　【例题】如下图所示，某城镇共有6条东西方向的街道和6条南北方向的街道，其中有一个湖，街道在此变成一个菱形的环湖大道。现在要从城镇的A处送一份加急信件到B处，为节省时间，要选择最短的路线，共有多少种不同走法？
　　A.35            B.36                C.37                D.38

　　
 
 
　　【例题】一条执行考察任务的科考船，现从B地沿河驶向入海口，已知B地距入海口60千米，水速为每小时６千米，若船顺流而下，则用4小时可以到达入海口，该船完成任务从入海口返回并按原速度航行4小时后，由于海水涨潮，水流方向逆转，水速变为每小时3千米，则该船到达Ｂ地还需再航行多少小时？
　　A.5      B．4    C.3    D.2

　　【例题】某单位组织职工参加团体操表演，表演的前半段队形为中间一组5人，其他人按8人一组围在外圈；后半段队形变为中间一组8人，其他人按5人一组围在外圈。该单位职工人数150人，则最多可有多少人参加？
　　A．149            B．148              C．138             D．133

　　山东公务员考试网(http://www.sdgwy.org/）解析

　　【解析】Ａ。此题求学生最多有多少人，相当于求得分情况最多有多少种。因为每道题的得分都不超过７分，所以3６＝2×3×６＝3×3×4＝１×６×６。任意两人各题得分不完全相同，而2×3×６有６种不同排列，3×3×4和１×６×６各有3种不同的排列，因此共有６＋3＋3＝１2种不同的排列，即有12种得分情况，所以这群学生最多有１2人。

　　【解析】C。放1个小球的盒子数与放2个和3个小球的盒子总数一样多，说明放1个小球的盒子有16÷2=8个，那么放2个和3个小球的盒子也有8个且一共放27-8=19个小球，由“鸡兔同笼”原理可知，放2个小球的盒子有（8×3-19）÷（3-2）=5个。

　　【解析】A。从A点到B点，要选择最短的距离有
　　①A→CF→B。A→C有5种方法；F→B有1种方法。共5×1＝5种方法。
　　②A→DE→B。A→D有10种方法；E→B有3种方法。共10×3＝30种方法。
　　从A到B的最短路线总共有5+30＝35种走法。
　　名师点评:最短路线决定了只能经过DE与CF，然后再分情况讨论。

　　【解析】B。此题为流水问题。路程为60千米，水速为6千米/小时，因为船顺流而下到达入海口用时4小时，所以船速为60÷4－6=9千米/小时。逆流航行4小时，该船行驶的路程为（9－6）×4=12千米，此时水流方向逆转，且水速变为3千米/小时，则剩余路程用时（60－12）÷（9＋3）=4小时。

　　【解析】D。队形如图所示，题目可理解为参加表演的人数减去5，可以被8整除；减去8可以被5整除。将选项代入，可知只有133符合题意，选D。