注意:单循环赛,即任意两队打一场比赛,和顺序无关,所以是组合问题;双循环赛,即任意两个队打两场比赛,和顺序有关,所以是排列问题。
例1.100名男女运动员参加乒乓球单打淘汰赛,要产生男、女冠军各一名,则要安排单打赛多少场?( )
A.90 B.95 C.98 D.100
【解析】设有男运动员a人,女运动员b人。因为是淘汰赛,则要产生男冠军需要a-1场比赛,产生女冠军需要b-1场比赛,总的比赛场次需要a+b-2场。
例2.足球世界杯决赛圈有32支球队参加,先平均分成八组,以单循环方式进行小组赛;每组前两名的球队再进行淘汰赛。直到产生冠、亚、季军,总共需要安排( )场比赛。
A.48 B.63 C.64 D.65
【解析】首先将32人平均分成八组,则每组有4支球队,每组球队要进行单循环赛,则每组有C24,则八组总共需要C24×8=48种;又因为在小组赛中每组决出前两名,八组一共决出16支队,也就是再对这16支队伍进行淘汰赛,直到产生冠、亚、季军,则有16场比赛。所以总比赛场次为48+16=64。
例3.8个甲级队应邀参加比赛,先平均分成两组,分别进行单循环赛,每组决出前两名,再由每组的第一名和另一组的第二名进行淘汰赛,获胜者角逐冠、亚军,败者角逐第3、4名,整个赛程的比赛场数是()
A.16 B.15 C.14 D.13
【解析】此题与例2的思路相同,不再赘述。
以上比赛计数问题的解题方法简单易懂,容易掌握,希望考生能举一反三,提高解题速度和答题的准确率。
二、错位排列问题
1、问题的提出
排列组合问题向来是考生备考行测数量关系的难点之一,而其中的错位排列问题更是让考生晕头转向。不过,虽然错位排列问题有难度,但是也有快速解决之道。为帮助考生攻克难关,国家公务员网公务员考试辅导专家总结多年教研心得,为考生们详细解析错位排列问题的答题方法。
错位排列问题是一个古老的问题,最先由贝努利(Bernoulli)提出,其通常提法是:n个有序元素,全部改变其位置的排列数是多少?所以称之为“错位”问题。大数学家欧拉(Euler)等都有所研究。下面先给出一道错位排列题目,让广大考生有直观感觉。
例1.五个编号为1、2、3、4、5的小球放进5个编号为1、2、3、4、5的小盒里面,全错位排列(即1不放1,2不放2,3不放3,4不放4,5不放5,也就是说5个全部放错)一共有多少种放法?
【解析】直接求5个小球的全错位排列不容易,我们先从简单的开始。
当小球数/小盒数为1~3时,比较简单,而当为4~6时,略显复杂,考生们只需要记下这几个数字即可(其实0,1,2,9,44,265是一个有规律的数字推理题,请考生们想想是什么?)由上述分析可得,5个小球的全错位排列为44种。
上述是最原始的全错位排列,但在实际公务员考题中,会有一些“变异”。
例2.五个瓶子都贴了标签,其中恰好贴错了三个,则错的可能情况共有多少种?
【解析】做此类题目时通常分为两步:第一步,从五个瓶子中选出三个,共有C53种选法;第二步,将三个瓶子全部贴错,根据上表有2种贴法。则恰好贴错三个瓶子的情况有C53×2=20种。
接下来,考生们再想这样一个问题:五个瓶子中,恰好贴错三个是不是就是恰好贴对两个呢?答案是肯定的,是。那么能不能这样考虑呢?第一步,从五个瓶子中选出二个瓶子,共有 种选法;第二步,将两个瓶子全部贴对,只有1种方法,那么恰好贴对两个瓶子的方法有 种。
问题出来了,为什么从贴错的角度考虑是20种贴法,而从贴对的角度考虑是10种贴法呢?
答案是,后者的解题过程是错误的,这种考虑只涉及到两个瓶子而没有考虑其他三个瓶子的标签正确与否,给瓶子贴标签的过程是不完整的,只能保证至少有两个瓶子的标签是正确的,而不能保证恰有两个瓶子的标签是正确的。所以国家公务员网公务员考试辅导专家建议各位考生在处理错位排列问题时,无论问恰好贴错还是问恰好贴对,都要从贴错的角度去考虑,这样处理问题简单且不易出错。
2 建立数学模型
1) 同室四人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡。则四张贺年卡的不同分配方式有
A. 6 种 B. 9 种 C. 11 种 D. 23 种
2)有5 个客人参加宴会,他们把帽子放在衣帽寄放室内,宴会结束后每人戴了一顶帽子回家。回家后,他们的妻子都发现他们戴了别人的帽子。问5个客人都不戴自己帽子的戴法有多少种?
其实就是n 个不同元素的一类特殊排列问题,本文试就给出这类问题的数学模型及求解公式。为方便,我们先把n 个不同的元素及相应的位置都编上序号1, 2, ...... , n,并且约定:在n 个不同元素的排列中
1. 若编号为i(i = 1, 2, ......, n) 的元素排在第i 个位置,则称元素i 在原位;否则称元素i 不在原位。
2. 若所有的元素都不在原位,则称这种排列为n 个不同元素的一个错排(若每个元素都在原位则称为序排)。按照上面约定,即为n 个不同元素的错排问题,则可构建“装错信封问题”的数学模型为在n 个不同元素的全排列中,有多少种不同的错排?
3 模型求解
应用集合中的容斥原理,我们就可得到“装错信封问题”的数学模型的求解公式。
设I 表示n 个不同元素的全排列的集合


4 应用举例
一个元素的错排数显然为0,二个不同元素的错排数为1,三个不同元素的错排数为2,均可由公式验证。由公式还可求得四个不同元素的错排数为9,五个不同元素的错排数为44。
则问题1)共有9 种不同的分配方式,故选(B)。问题2)共有44种不同的戴法,下面再举几例说明公式的应用。
1. 某省决定对所辖8 个城市的党政一把手进行任职交流,要求把每个干部都调到另一个城市去担任相应的职务。问共有多少种不同的干部调配方案?
解答:实质上本题即为8 个不同元素的错排问题,一种干部调配方法对应于8 个不同元素的一个错排。故由公式可求得不同的干部调配方案数为
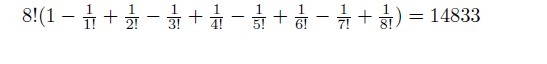
错位排列问题是排列组合问题里比较模糊、棘手的题型,所以考生们对错位排列问题一定要善于总结规律,熟能生巧,才能在临考时,准确抓住解题的突破口。
行测更多作答思路和作答技巧,可参看2013年公务员考试技巧手册。












