一些排列组合问题条件比较多，直接使用分类或分步来考虑较为复杂，在这种情况下，掌握一些特定的解题方法和公式有助于大家快速解题。在此，专家介绍七种解题方法，其适用范围如下：

　　1.特殊定位法

　　排列组合问题中，有些元素有特殊的要求，如甲必须入选或甲必须排第一位；或者有些位置有特殊的元素要求，如第一位只能站甲或乙。此时，应该优先考虑特殊元素或者特殊位置，确定它们的选法。

　　例题1： 1名老师和6名学生排成一排，要求老师不能站在两端，那么有多少种不同的排法？

　　A．720    B.3600    C.4320    D.7200

　　解析：此题答案为B。此题中特殊元素是老师，特殊位置是两端，可优先考虑。

　　2.反面考虑法

　　有些题目所给的特殊条件较多或者较为复杂，直接考虑需要分许多类，而它的反面却往往只有一种或者两种情况，此时我们先求出反面的情况，然后将总情况数减去反面情况数就可以了。

　　例题2： 从6名男生、5名女生中任选4人参加竞赛，要求男女至少各1名，有多少种不同选法？

　　A．240    B.310    C.720    D.1080

　　解析：此题答案为B。从反面考虑，“男女至少各1名”的反面是“只选男生或只选女生”。

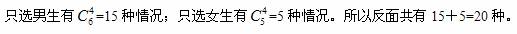
　　从6名男生、5名女生中任选4人的所有情况共有=330种。

　　故所求为330-20=310种不同选法。

　　3.捆绑法

　　在排列问题中，如果题中要求两个或多个元素“相邻”时，可将这几个元素捆绑在一起，作为一个整体进行考虑。

　　例题3： 6个人站成一排，要求甲、乙必须相邻，那么有多少种不同的排法？

　　A．280    B.120    C.240    D.360

　　4.插空法

　　在排列问题中，如果题中要求两个或多个元素“不相邻”时，可先将其余无限制的n个元素进行排列，再将不相邻的元素插入无限制元素之间及两端所形成的（n+1）个“空”中。

　　如果所有元素完全相同，即为组合问题，则不需要进行排列，只需要将不相邻的元素插入空中即可。

　　例题4： 6人站成一排，要求甲、乙必须不相邻，有多少种不同的排法？

　　A．240    B.480    C.360    D.720

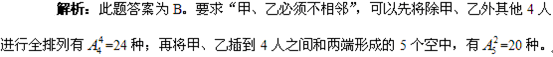
　　由乘法原理，不同的排法共有24×20=480种。

　　5.隔板法

　　例题5： 将10台相同的电脑分配给5个村，每村至少一台，那么有多少种不同的分配方法？

　　A．126    B.320    C.3024    D.1024

　　解析：此题答案为A。10台电脑并成一排，中间形成9个空，在这9个空中任意插入4个板，就把这10台电脑分成了5部分，每一种插法就对应一种分配方法，故有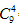种分法。

　　6.归一法

　　排列问题中，有些元素之间的排列顺序“已经固定”，这时候可以先将这些元素与其他元素进行排列，再除以这些元素的全排列数，即得到满足条件的排列数。

　　例题6： 一张节目表上原有3个节目，如果保持这3个节目的相对顺序不变，再添进去2个新节目，有多少种安排方法？

　　A.20                 B.12                 C.6                 D.4

　　解析：此题答案为A。“添进去2个新节目”后，共有5个节目，因此，此题相当于“安排5个节目，其中3个节目相对顺序确定，有多少种方法？”

　　由于“3个节目相对顺序确定”，可以直接采用归一法。

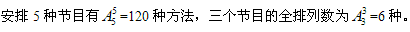
　　所以，一共有120÷6=20种安排方法。

　　7.线排法

　　排列问题一般考查的是直线上的顺序排列，但是也会有一些在环形上的顺序排列。与直线排列问题相比，环形排列没有前后和首尾之分，此时我们只需要将其中一个元素列为队首，这样就可以把环形问题转为线形问题。

　　例题7： 某小组有四位男性和两位女性，六人围成一圈跳集体舞，不同的排列方法有多少种？

　　A．720    　　       B．60   　　      C．480  　　         D．120

　　解析：此题答案为D。本题考虑了次序，属于排列问题。但由于围成一圈，是没有首尾之分的，所以可以将其中一个人列为队首，对其余5个人的次序进行排列。

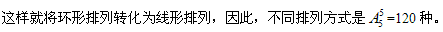
　　通过对上述例题的讲解，大家可以发现，排列组合问题一般可一题多解，解题的基本思想都是把复杂的问题简单化。除了基本的“分类”和“分步”方法外，上述这几个方法也是比较常用的，需要牢记：特殊条件优先考虑，复杂问题反面考虑，元素相邻用捆绑法，元素间隔用插空法，元素分组用隔板法，元素定序用归一法，环形问题用线排法。

　　行测更多解题思路和解题技巧，可参看2013年公务员考试技巧手册。