在公务员考试中,数学运算部分一直是必考内容,主要考查应试者理解和解决数量关系问题的技能。根据历年应试者的信息反馈,专家发现,数学运算常因其计算量大、耗时多等原因成为被很多考生放弃的部分。
事实上,公务员考试中的数学运算题并非单纯的考查应试者的计算能力,更多是如大纲中提到的对考生分析问题和合理应用各种解题方法快速答题的考查。
如下面这道2010年联考真题:
【例题】一列队伍沿直线匀速前进,某时刻一传令兵从队尾出发,匀速向队首前进传送命令,他到达队首后马上原速返回,当他返回队尾时,队伍行进的距离正好与整列队伍的长度相等。问传令兵从出发到最后到达队尾所行走的整个路程是队伍长度的多少倍?
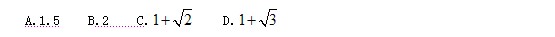
该题的特点是数量关系叙述清楚,但题干中涉及的计算数据极少,给人以无从下手的感觉。如果按照以往的解题思路,虽然也能够得出正确答案,但需要大量的时间,根本不能适应时间紧迫的考场。从命题者的角度考虑,必定有一种巧妙的解题思路,能够快速的得出答案。
【解析】首先阅读题干可知,这是一道关于行程的问题。行程问题的核心概念是相同时间内路程比等于速度比。抓住该核心概念在题目中寻找解题的关键点,即队伍行进的时间等于传令兵从队尾出发到返回队尾所用的时间。

该题中使用了一种在数学运算中常用的解题方法,特值法。特值法是通过对某一个未知量取一个特殊值,将未知值变成已知量来简化问题的方法。最适合数量关系清楚而题干数据极少的题目。
如2010联考真题:
【例题】单独完成某项工作,甲需要16小时,乙需要12小时,如果按照甲、乙、甲、乙、……的顺序轮流工作,每次1小时,那么完成这项工作需要多长时间?
A.13小时40分钟 B.13小时45分钟
C.13小时50分钟 D.14小时

常用的特值法有特殊数值、特殊数列、特殊函数、特殊方程、特殊点等。一般,首先假设出一个特殊值,然后将特殊值代入题干,通过一系列数学运算得出结论;有时候也会通过检验特例、举反例等方法来排除选项。使用特值法不仅可以减少计算量,同时可以简化解题思路,无需考生耗费大量的时间进行推导,适用范围广,所以考生应重点掌握特值法。










